＜猫の鳴き声を作る＞　

国際基督教大学　坂口権司

一般教養「物理学の基礎と概念」課題研究　（岡村准教授）

 

実験：ネコの鳴き声を作る

 

目的：　ネコの鳴き声に近い音を作成する

　　

方法：　「効果音エディタ＿Ｄ」と「WinSona」の二つのフリーソフトを使用した。

　　　　　　「効果音エディタ」は効果音を作るためのソフトで、このソフトを使って

　　　　　　ネコの鳴き声に近い音の作成を試みる。

　　　　　　「WinSona」は音の周波数分布をスペクトログラムで表示するソフトで、

　　　　　　作った音をチェックするために使った。

 

 

　効果音エディタの初期画面。

 

まずは音をつくってみる

　

　　　　　　音を作るために最初に必要なことは波形を決めることだ。

　　　　　　波形を作る方法は「手描き」と「倍音作成機能」の二つがある。

　　　　　　試しに「手書きで」波形を描いてみると以下のようになった。

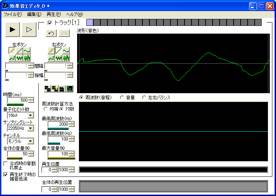
　「手描き」で波形を描いた図

 

　再生ボタン（左上の三角形のボタン）を押すとちゃんと音が鳴った。音が作れた！

　しかし、手描きではいつでも同じ音を作ることが不可能だし恣意的になってしまう。

　

　そこで「倍音作成機能」を使って波形を作っていくことにしたい。

 

　倍音作成機能を選択すると、次のようなウィンドウがあらわれる。

 

　　倍音作成ウィンドウ　↓

 

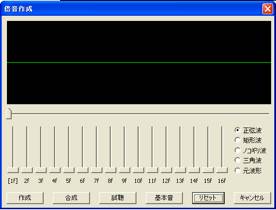
　１ｆから１６ｆまでのボタンがあり、これらを操作することで様々な波形を作ることができる。

　

　（例１）Ｆ１のツマミを上げる　↓

 

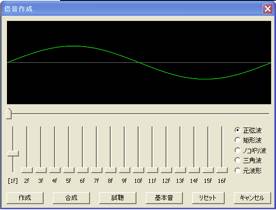
（例２）Ｆ１とＦ４のツマミを上げる　↓

 

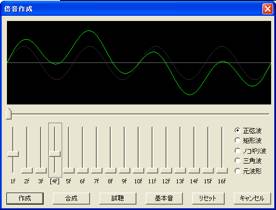
　「倍音作成機能」を使えば様々な波形を簡単に作れることがわかった。

　では、「倍音作成機能」にある１ｆとか３ｆという記号は何を意味しているのだろうか？

 

　周波数を一定にし、「倍音作成機能」にあるＦ１などのボタンを変えることで実際に作った音にどのような変化がみられるか実験してみた。

 

　まず、最高周波数と最低周波数をともに1000Ｈzに設定した。（初期設定は最高周波数2000Ｈz、最低周波数100Ｈz）

　こうすることで1000Ｈzの音を作ることができるのではないかと考えた。

 

　←初期設定

 

　←両方とも1000Ｈzに

 

 

 

　次に、「倍音作成機能」でＦ１のツマミを上げた。

 

 

　この音を音声解析ソフト「WinSona」で見てみると以下のようになった。

 

最高周波数・最低周波数ともに1000Hz　波形１ｆ↓　

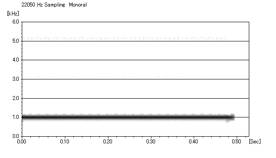
　　　　1000Hzのところに一本の線が見られる。

　　　　つまり1000Hzの音を作ったということがわかる。

 

　では次に、最高周波数・最大周波数は1000Ｈｚのままで、Ｆ１の代わりにＦ２のツマミを上げてみた。

　その音を「WinSona」で見てみると以下のようになった。

 

最高周波数・最低周波数ともに1000Hz　波形２ｆ　↓

　

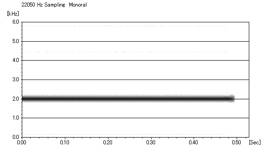
　2000Hzのところに一本の線がみられる。

　つまり2000Hzの音を作ったということになる。

 

　

　周波数を1000Hzに設定し、

　１ｆの波形のときは1000Hzの音ができ、

　２ｆの波形のときは2000Hzの音ができた。

 

　このことからＦ１〜Ｆ１６を使うことで基本となる周波数（今回の場合は1000Hz）の整数倍の周波数の音を

　作ることができる、ということが分かった。

 

　広辞苑によると、

　　　　「振動体の発する音のうち、基音の振動数の整数倍の振動数をもつ部分音」

　のことを倍音という。

　

　「倍音作成機能」とは基本となる周波数の整数倍の音をつくる機能であり、１ｆ〜１６ｆの数字はその倍数を

　あらわす数字であるということがわかった。

 

「効果音エディタ」では倍音を恣意的に選択して音をつくることができるということになるが、その時に注意

しなければいけないことは、もし音の作成上の基本となる音を1000Hzに設定し倍音作成でＦ２とＦ３を選ん

だ場合には、実際の音の基音は2000Hzとなるということである。

　

 

 

　基本となる周波数をきちんと把握することが大切である。

　これまでは最高周波数と最低周波数を同じにすることで周波数を固定化していた。

　しかしこのような方法では音に抑揚をつけることができない。

　「効果音エディタ」では音程の抑揚をつけることができる（手描き）。

　　

　　（例）音程の抑揚を描いた　↓

　

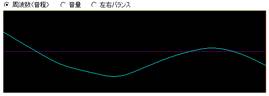
この抑揚をつけるためのグラフは縦軸を周波数、横軸を時間としている。

最高周波数と最低周波数の選択した値が、このグラフの上限と下限になる。

だから、最高周波数と最低周波数を同じ値にしてしまうと音程の抑揚がつけられない。

 

では仮に最高周波数を3000Hz、最低周波数を1000Hzとした場合の基本となる周波数は

どうなるのか？

 

そのとき重要になるのが周波数計算方法だ。

　　　　　　　　　　　　　　　　　　　　　　　　

　←これ

 

初期設定では「対数」が選択されている。

 

では、周波数計算方法がそれぞれどのようになっているのか調べてみよう。

最高周波数を3000Hz、最低周波数を1000Hzとし波形は１ｆとする。これまでの実験で「倍音作成機能」でＦ１

を選択すれば基本となる音が作れることがわかっているので、周波数計算方法を「均等」にした時と「対数」に

した時の音の周波数を見ればどのような計算方法をしているのかが分かるはずだ。

 

まず周波数計算を「均等」にした方を「WinSona」で見てみると以下のようになった。

 

最高周波数3000hz　最低周波数1000Hz　波形１ｆ　周波数計算「均等」

 

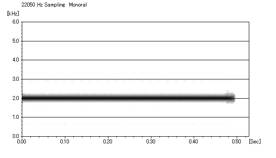
2000Hzのところに一本の線が見られた。

このことから周波数計算を「均等」すると、基本となる周波数は最高周波数（3000Hz）と最低周波数（1000Hz）

の平均の値（2000Hz）となることが分かった。

 

次に、周波数計算を「対数」にした方を「WinSona」で見てみると以下のようになった。

 

最高周波数3000Hz　最低周波数1000Hz　波形１ｆ　周波数計算方法「対数」

 

 

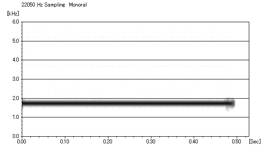
1700Hz付近に一本の線が見られた。

一見したところ計算方法がわからないので、最高周波数と最低周波数を違う数値にしてなんどか試して

みたが全く検討がつかなかった。

「対数」を使った複雑な計算をしているのだろうか。

 

周波数計算方法に関して、「対数」はその方法がわからなかったが、少なくとも「均等」に関しては最高・最低

周波数の平均値が基本となる周波数となることがわかったので、以後は周波数計算方法を「均等」にして音

の作成をしていくことにする。

 

 

 

これまでのところで音を作るための操作を理解したので、いよいよネコの鳴き声の作成に取りかかることにする。

 

ネコの鳴き声を作成するにあたって本物のネコの鳴き声を参考にすることにした。

ここではモデルとしてkitten3.wavを選んだ。（音源はhttp://www.kessels.com/CatSounds/index.htmlから）

 

kitten3.wav ↓

 

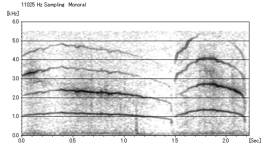
この鳴き声は、主に1000Hzの基音とその倍音（2000Hz、3000Hz、4000Hz）によって構成されている。

一回目の鳴き声（0.0secから1.5secまで）を参考にして、鳴き声の作成を試みることにした。

 

 

まず、基本となる周波数を1000Hzにするために、最高周波数を1900Hz、最低周波数を100Hzにした。

（平均が1000Hzになればどんな数値にしても変わらないが、後で音程の抑揚をつけるときに、この

　方がやりやすいと考えた。）

次に、波形は「倍音作成機能」で１ｆ、２ｆ、３ｆ、４ｆを選択した。

 

この時点で作ったおとを聞いてみると「ピー」というサイレンのような音がした。猫の鳴き声とは程遠い。

これを「WinSona」で見てみると以下のようになる。

 

 

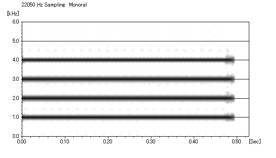
さらに周波数を時間軸にそって低く山型にし（手書き）音程の抑揚をつけ、kitten3.wavに近づけてみた。

 

 

 

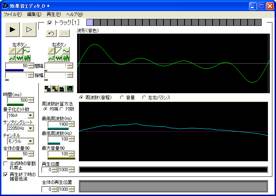
聞いてみると、鳴き声らしいおとになった！さっきのサイレンのような音からするとまるで違う。

「WinSona」で見てみると以下のようになる。

 

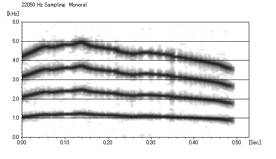
さらに、音の時間を初期設定の500msから1500msにしてkitten3に近づけた。

　　　　　　　　　　

聞いてみると、とくに劇的な変化はみられない。音が長くなった分だけ音程の抑揚の細かい部分が気になり、

少し調整。

 

 

最後に、音量を時間軸に沿って山型にして声を出している感じを演出した。それまでは一定音量であった。

 

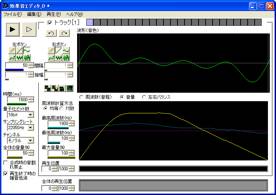
聞いてみると、よりリアリティが感じられた。

「WinSona」で見てみるといかのようになった。

 

 

 

 

 

 

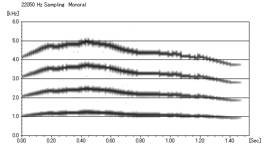
　　このようにWinsonaのスペクトログラムを参考にして、ある程度ねこの鳴き声に近い音が作れることがわかった。

　　その際に、音程や音量の抑揚が重要なことがわかった。また、周波数や音量の線画のときに丸みをもたせる

　　と、より滑らかでリアリティが増す。