スカートのめくれやすさ
物理の世界(A) - 科学的な考え方
2014/11/20
(指導教員 岡村秀樹)
自由研究グループ10
青田麻弥、中莖暁、深澤冠、稲田知美、S.K.
黄田瑞貴、東郷友紀、築地まどか、山崎ひとみ、吉原楓、広岡沙良
《序論 Introduction》
●目的
スカートのめくれやすさに最も大きく影響する要因を、環境的な要因とスカートそのものの要因の2つの視点から検証する。また、我々がスカートがめくれやすい状況に置かれた時に、簡単に実践できるスカートをめくれなくする方法を探る。●先行研究
風によってスカートがめくれる現象について、科学的に検証した文献は非常に少なかったため、まず風の性質を調べた。まず、風の吹く仕組みについては、風は、対流によって発生する。空気は太陽熱によって(地表が暖められてそれによって空気が)暖められると膨張し軽くなるため、上昇する。逆に冷えた空気は縮小するため、上空で冷えた空気は縮小して重くなることで下降する。この対流によって風が発生する。すなわち、気温の高いところでは空気が軽くなるため低気圧ができ、気温の低いところでは空気が重くなり高気圧ができ、空気が気圧の高いところから低いところに流れ、風が吹くということである。気圧の差が大きいほど強い風が吹くということになる(なかのひろみ 2002)。
また、風はその規模によって、大規模な風系、中規模な風系、小規模な風系という3つに分けられることが多いという。場所や時間によって変化する最も人にとって身近な小規模な風系は、隣り合った空気の微妙な温度差や微妙な気圧差によって引き起こされ、海風陸風、山風谷風や季節風に代表される中規模な風系は、水の温度変化にかかる時間と地面の温度変化にかかる時間の差によって気圧差が生まれることで発生し、また、極偏東風や偏西風、貿易風等の大規模な風系は、気圧差によって発生する風に、コリオリ力が影響しているのだという(なかのひろみ 2002)。 風によってスカートがめくれる現象を、科学的に検証している学術論文を見つけることはできな かったが、ブログで検証を試みているものを見つけることができた。そこには以下のような示唆が述べられていた。送風機で様々なスカートに風をあて、スカートがめくれやすい条件を調べる実験によって、横から風が吹くような場所ではスカートはめくれづらいが、下から風が吹くような場所ではスカートが風でめくれやすいという結果が得られたという。
例として、このような下方向から風が吹く場所として、地下鉄駅のホームへの階段が挙げられ、駅に近づいてくる列車が空気を圧縮し・ホーム近くの気圧を高めるため、ホームと上階の間の階段やエスカレータで、上階への風が吹くという。ベルヌーイの定理を使うと、下から吹く風がスカートを持ち上げようとする力は、空気の密度 × スカートに下部から風が吹き込む面積 × 風速 × 風速 / 2 で見積もることができ、列車によって吹く風は大きく見積もっておよそ5m、一般的なスカートの重さはおよそ100?350g程度だということを加味すると、一般的なスカートであればスカートを持ち上げようとする力よりもスカートの重力の方が大きいためスカートは持ちあがらないという結論をだしている。また、階段を上り下りしている場合は風速に人の速さが加わり、また、気温や気圧によって空気の密度が変化するため、これらの諸条件によって結果が変わると述べられている。
この先行研究の結果から、気圧や気温によって風は変化するが、小規模な風系は身近な空気の温度差や気圧差で発生し、スカートがめくれるような風もこの風に分類される。そのなかでも下から上に向かって吹く風によって、スカートがめくれる現象が起き、(空気の密度は大きく変動しないため)それは風速やスカートの重さ、スカート下部から風が吹き込む面積に大きく左右されるという示唆が得られた。
しかしこれらの結果は、具体的に風速やスカートの種類、下部から風が吹き込む面積という条件を変えながら実験して得られたものではなく、スカートがめくれる現象への考察が不十分であり、我々はより身近な諸条件によってどのようにスカートがめくれる現象が影響されるのか調べた。
〈参考文献〉
なかのひろみ,2002,『風はどこで生まれるの?』アリス館.
平林純,2014,「風でめくれるスカート」の科学!「涼しく晴れた朝の地下鉄駅をドジっ娘が走る」とスカートは必ずめくれる!?の法則」,雑学界の権威・平林純の考える科学,2013年7月15日,(2014年11月9日取得,http://hirabayashi.wondernotes.jp/).
予備実験 「風が通る地面の角度とめくれやすさの関係」
《方法 Methods》
予備実験では、女子高校生の制服に用いられる一般的なスカートを研究対象として固定し、スカートを履いている人が立っている地形によりスカートのめくれやすさに変化があるかどうか調査した。具体的には、台の上に置いたトルソーに制服のスカートを履かせ、その台までダンボールで坂を作り、坂の下から地面と水平方向に扇風機で風を送り、坂の角度によりスカートのめくれかたに変化があるか実験を行った。この実験は、実際の地形や街中での状況を想定しており、スカートがめくれる原因が下からの風であるのではないかという考えのもと、地下鉄の階段など立っている場所の角度が急であるほど、下方向からの風の成分が多くなると考えられるため、めくれやすくなるという仮説を立てて行われた。坂の角度は15°、30°、45°、60°、75°、90°に設定した。
《結果 Results》
15°が最もめくれ方が小さく、90°が最もめくれ方が大きいと想定していたが、実験の結果、15°~60°までは角度がきつくなるにつれめくれ方が大きくなっていくことが確認できたが、60°以降はあまり大きな差が見られなかった。そこで、坂の角度により下方からの風速が変化しているかを見ると(表1)、45°~60°以外では大きな差が見られなかった。| 坂の角度(°) | 15 | 30 | 45 | 60 | 75 | 90 |
|---|---|---|---|---|---|---|
| 風速(m/s) | 1.7 | 1.7 | 1.8 | 2.2 | 2.2 | 2.1 |
原因としては、この実験装置としてダンボールを手で支えて斜面を作っていたため不安定であったことや、坂の角度どおりに風が曲がっているとは限らない事、また、スカートの形状と風の角度の関係について考慮に入れていなかったことなど様々なものが考えられた。そこで、この実験ではスカートの種類を一種類に固定した上で下からの風のみに焦点をあてていたが、次の本実験ではスカートの重さや長さなどといった要素に焦点をあて、それらの要素がめくれ易さにどう影響するかを調べることにした。
実験1「スカートにおける要素とめくれやすさとの関係」
《方法 Methods》
予備実験においては、スカートのめくれやすさには風の角度が影響しているということがあまりはっきりしなかった。そのため、今度はスカートのめくれやすさがスカートそのものの要素によって変化することに着目し、次の仮説として、「スカートの長さ、重量、裾の周囲の長さ、の3つの要素がめくれやすさに影響する」、と考えた。そこで、今回の実験では、風の種類を垂直真下方向からの風速○m/sの風に統一し、扇風機の上にスカートをはかせたトルソーを設置。10秒間風を送り、13種類のスカートによるめくれ方の違いを観察した。前回の実験でめくれ方を客観的に観察できなかった反省を活かし、今回の実験ではトルソー本体にビニールテープで5cmの間隔で目盛を付け、スカートがめくれることによってどの目盛までが確認できたかを数値で表すようにした。この際、視点の高さによって観測できる数値が変わってしまうことを避けるため、13のスカートにおいて同一の観測者が観測した。また、1つのスカートにつき2回同じ実験を繰り返した。尚、使用した13種類のスカートは以下の通りである。 1(紺フェルト) 1(紺フェルト) |
 2(グレーヒラヒラ) 2(グレーヒラヒラ) |
 3(白グレーストライプ) 3(白グレーストライプ) |
 4(長い青白花) 4(長い青白花) |
 5(白黒ストライプ) 5(白黒ストライプ) |
 6(白クリームストライプ) 6(白クリームストライプ) |
 7(茶色花柄) 7(茶色花柄) |
 8(黒) 8(黒) |
 9(グレー) 9(グレー) |
 10(白デニム) 10(白デニム) |
 11(黒模様) 11(黒模様) |
 12(ジーンズ柄ロング) 12(ジーンズ柄ロング) |
 13(黒裾フリフリ) 13(黒裾フリフリ) |

《結果 Results》
各スカートのめくれ具合は以下の通り。| スカート名称 | めくれやすさ |
|---|---|
| 1.紺フェルト | 全くめくれない |
| 2.グレーひらひら | 3つ目の線 |
| 3.白グレーストライプ | 1つ目の線 |
| 5.白黒ストライプ(もともと3つ目) | 6つ目の線、時々7つ目;4つ目 |
| 6.白クリームストライプ(もともと2つ目) | 2つ目 |
| 7.茶色花柄 | 2つ目;時々3?4つ目 |
| 8.黒 | 時々1つ目 |
| 9.グレー | めくれはしない;広がらない |
| 10.白デニム(もともと2つ目) | めくれはしない;広がらない |
| 11.黒模様 | 7つ目 |
| 13.黒裾フリフリ | 時々1つ目;時々1?2つ目 |
| 4.長い青白花 | めくれはない;広がる |
| 12.ジーンズ柄ロング | 広がるが、めくれない |
地面から何cmのところまでが見えたかを、めくれやすさ定数(H)と定義し、Hと(スカートの長さ、重量、裾の周長)の関係を表にすると以下のようになった。
| スカート名称 | H | 長さ(cm) | 重さ(g) | 周長(cm) |
|---|---|---|---|---|
| 1.紺フェルト | 64.5 | 37.5 | 288 | 109 |
| 2.グレーひらひら | 60 | 40 | 190 | 107 |
| 3.白グレーストライプ | 50 | 46 | 189 | 181 |
| 5.白黒ストライプ(もともと3つ目) | 73.333 | 34 | 198 | 204 |
| 6.白クリームストライプ(もともと2つ目) | 55 | 45 | 158 | 136 |
| 7.茶色花柄 | 60 | 57 | 155 | 162 |
| 8.黒 | 50 | 57 | 247 | 165 |
| 9.グレー | 64 | 38 | 170 | 84 |
| 10.白デニム(もともと2つ目) | 62.5 | 39.5 | 273 | 88 |
| 11.黒模様 | 80 | 40 | 136 | 230 |
| 13.黒裾フリフリ | 51.667 | 49 | 198 | 173 |
| 4.長い青白花 | 20 | 82 | 176 | 168 |
| 12.ジーンズ柄ロング | 30 | 72 | 243 | 206 |
(長さ、重量、裾の周長)とHのそれぞれの相関を散布図で表したところ、長さとHは負の相関、裾の周長とHは正の相関を示した。(*1)これはつまり、短く、裾の周長が大きいスカートほどHの値は大きくなる、ということである。ここでは重量とHの相関関係は見られなかったが、経験上軽い素材よりも重い素材の方がめくれにくいということや、同じスカートでも裾に重りを取り付けるとめくれにくくなるという実験結果から、重量も十分な程度でHに影響を与えるとして良いと判断した。
重量とHに関して相関が見られなかった原因としては、集められたスカートのバリエーションに偏りがあったことが考えられる。
また、ここで行なったのはHと各項目1つずつについての相関関係であり、長さ、重量、裾の周長の相互の間の相関関係などを考えておらず(密度が一定ならば長くするほど重くなる、など)、後述の方程式導出の際にはそういった点にも考慮し、3変数を定義した。
(*1)正確には周長とHの相関には疑問が残るが、相関を示さないロングスカート(右下2点)を除くとすっきりとするので、この段階では正の相関だと考えておく。後述の周長(半径)と長さとの関係で考える際に改めて確認していただきたい。


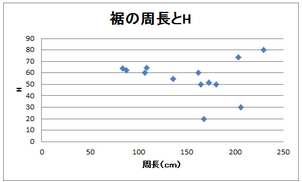
次に、このスカートの種類に関する3つの数値と実験から得られたデータを用いて、スカートの素材と形によるめくれやすさを表す方程式を作成できないかと考え、(x,y,z)={密度(重量/長さ),開き角をθとした時のtanθ(裾が広がった時の半径/長さ),長さ}を3変数としておき、数式処理システムmathematicaを使用して方程式を導いたところ、次のような方程式が得られた。
H = 103.613 - 1.34959 x + 15.4753 y - 1.02725 z
(めくれやすさ) (密度) (tangent) (長さ)
(tangentを使用したことについて)
周長とHの相関、tangentとHの相関関係について、簡易的ではあるが散布図で比較してみると、明らかにtanを使用したほうが明らかな相関が得られたので、tangentを使用するのは妥当性が高いと考えられる。
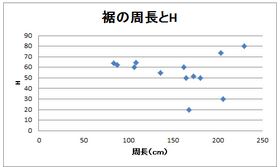
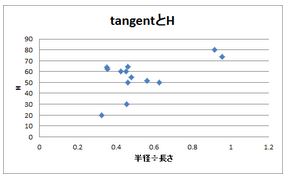
(導き出された方程式についての検証)
まず、密度と長さについての係数が負となり、開き角(半径/周長)についての係数は正の数になっていて、前述の傾向と一致する。
また、f =103.613-1.34959x+15.4753y-1.02725z とし、x,y,zに実際に3つの数値を代入することで得られたf の値をHの値と比較すると、以下の通りで、今回のデータに関してはこの方程式によって実際の測定結果から遠くないHの値が導き出されると言って良いだろう。
| スカート名称 | H | f |
|---|---|---|
| 1.紺フェルト | 64.5 | 61.88893919 |
| 2.グレーひらひら | 60 | 62.70423532 |
| 3.白グレーストライプ | 50 | 60.51061443 |
| 5.白黒ストライプ(もともと3つ目) | 73.333 | 75.61244141 |
| 6.白クリームストライプ(もともと2つ目) | 55 | 60.09560923 |
| 7.茶色花柄 | 60 | 48.39338419 |
| 8.黒 | 50 | 46.34479435 |
| 9.グレー | 64 | 63.98708312 |
| 10.白デニム(もともと2つ目) | 62.5 | 59.1989862 |
| 11.黒模様 | 80 | 72.10365754 |
| 13.黒裾フリフリ | 51.667 | 56.5245091 |
| 4.長い青白花 | 20 | 21.53046436 |
| 12.ジーンズ柄ロング | 30 | 32.14654024 |
実験2「スカートをめくれなくする方法を探す」
次に、スカートをめくれなくする方法を探るため、スカートのウエストと裾の周長の比率に焦点を当てた実験を行った。《方法 Methods》
(手順①) 実験1で見つけた最もめくれやすいスカート(11番)のウエストと周長を計測(ウエスト66cm, 周長230cm)。ウエスト:周長=1:3.48という比を求めた。(手順②) 同スカートの裾をヘアピンでつまみ、周長を短くして実験1と同じ方法で扇風機の風をあて、スカートがめくれるかを調べた。



《結果 Results》
変えた周長とウエストとの長さ比、めくれる/めくれないの結果は以下のようになった。| 周長(cm) | ウエスト:周長 | 結果 |
|---|---|---|
| 190 | 1:2.89 | めくれる |
| 160 | 1:2.42 | めくれる |
| 150 | 1:2.28 | めくれない |
この結果を踏まえ、私達はウエスト:周長=1:2.3以下であればスカートはめくれなくなると考えた。そこで、実験1で使用した他のスカートのウエストと周長の比も計算し、その内比率が1:2.3より大きいものについて、1:2.3になるよう同じ方法で周長を短くし、再度風をあてて実験を行った。(元から対ウエストの周長比が2.3以下のものについては、めくれていなかった。)すると、他のスカートにおいても、ウエスト:周長を1:2.3に設定すればめくれなくなることがわかった。ただし、4番と12番の丈が長いロングスカートについては、同比率が2.3以上であっても元々めくれていないため、この比率は当てはまらない。
《議論 Discussion》
実験1で導き出せたスカートのめくれやすさ方程式と、実験2の結果より、スカートのめくれやすさには周長が最も大きく相関していることが見えてきた。しかし、一応以下に挙げる他の要素も考慮してみた。
一つ目は、スカートの重さとめくれやすさの関係についてである。ネット上にある記事によれば、10円玉のコインをスカートの裾に縫い付ければ、強風が吹いてもスカートはめくれないという情報を得た。従って、コインを縫い付ければ本当にめくれないのかを実験してみた。手順として、スカートの裾に10円玉を挟んで、スカートの下から風をあてた。最初は一枚の10円玉を挟んだが、風をあてたらスカートはめくれた。二回目は、二枚の10円玉を挟んでみた。そこでも一枚のコインの時のようにスカートはめくれた。そこで、スカートの前の部分と後ろの部分両方にコインを2枚ずつつけてみることにした。風をあてたら、コインによって重くなっている部分だけが固定されていて、他の部分はめくれた。まとめると、10円玉をスカートの裾に入れても、スカートがめくれないという情報は実際に証明できなかった。つまり、スカートの重さはめくれやすさとはあまり相関がないことがわかった。
二つ目は、スカートの内側と外側の風の圧力についてである。スカートの内側と外側の圧力を同じにしたらスカートはめくれないだろうと考えた。そこで、スカートにパイプのようなものを挟んで、内側の空気を外に流したら同じ圧力になるだろうと思われた。実際にスカートの後ろの部分にパイプのようなものを挟み、下から風をあてる実験をした。しかし、変化は見えず、スカートはめくれた。違うスカートでもやってみたが、やはりめくれる状態には変化がなかった。ここで、実際に内側の空気はパイプによって外に逃げ出せるのかを疑問に思い始めた。パイプの上の部分に手を当ててみたが、空気が外に流れているのは感じられなかった。まとめると、スカートの内側と外側の圧力の差によってスカートのめくり具合が変わるのかは明らかにできなかった。
《結論 Conclusion》
以上を踏まえ、今回の我々の実験からめくれやすさを数値化するための方程式が導き出せた。この方程式の妥当性も検証し、実際の測定結果に近い数値を数値計算で算出できることも示した。加えて、ウエストと裾の長さの比が1:2.3以下であれば、スカートはめくれないこともわかった。そして、我々が普段使っているヘアピンでスカートの裾をつまみ、周長を対ウエスト比2.3の長さに縮めるだけで、簡単にスカートをめくれなくすることができることも証明された。
一方で、風が通る地面の角度など、同じくめくれやすさに関係するであろう環境的な要因については、我々の実験ではきちんと検証することができなかった。今後、他の研究者の方々がこの部分の解明に乗り出していただけることを期待したい。